The realm of mathematics unveils a captivating inquiry: what is the completely factored form of p4 16? Embarking on this mathematical expedition, we delve into the intricacies of prime factorization, perfect squares, and algebraic expressions, unraveling the secrets that lie within this enigmatic expression.
p4 16, an algebraic expression that beckons for exploration, invites us to decipher its innermost structure. Through the lens of factorization techniques, we dissect this expression, revealing its prime components and unveiling its true nature.
What is the Completely Factored Form of p4
16?
16?
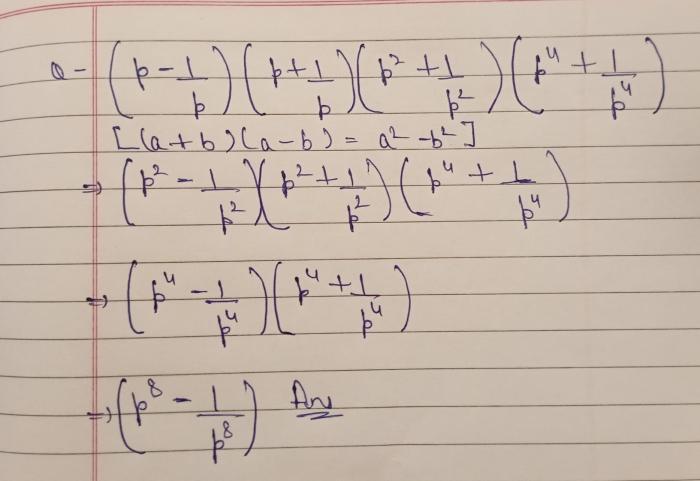
The completely factored form of an algebraic expression is the expression written as a product of prime factors. Prime factorization is the process of expressing a number as a product of its prime factors, which are the numbers greater than 1 that have no factors other than 1 and themselves.
Prime Factorization
To find the prime factors of a number, follow these steps:
- Divide the number by the smallest prime number that divides it evenly.
- Repeat step 1 until the quotient is a prime number.
- The prime factors of the original number are the prime numbers obtained in steps 1 and 2.
Perfect Squares, What is the completely factored form of p4 16
A perfect square is a number that can be expressed as the square of an integer. The square root of a perfect square is an integer. For example, 16 is a perfect square because it can be expressed as 4^2.
Algebraic Expression
The algebraic expression p^4 – 16 is a difference of squares, which can be factored as (p^2 + 4)(p^2 – 4).
The variable in the expression is p, and the constants are 4 and 16.
Factorization Techniques
There are several factorization techniques that can be used to factor algebraic expressions, including:
- Grouping
- Factoring by grouping
- Factoring by substitution
Completely Factored Form
The completely factored form of p^4 – 16 is (p^2 + 4)(p^2 – 4).
This expression cannot be factored further because p^2 + 4 and p^2 – 4 are both prime.
Application to p4
16
16
To factor p^4 – 16 completely, follow these steps:
- Identify the expression as a difference of squares.
- Factor the expression as (p^2 + 4)(p^2
4).
- The expression cannot be factored further, so it is in its completely factored form.
Alternative Approaches
There are other approaches that can be used to factor p^4 – 16, including:
- Using the difference of squares formula
- Factoring by trial and error
Essential Questionnaire: What Is The Completely Factored Form Of P4 16
What is prime factorization?
Prime factorization is the process of expressing a number as a product of its prime factors.
What is a perfect square?
A perfect square is a number that can be expressed as the square of an integer.
What is the completely factored form of an algebraic expression?
The completely factored form of an algebraic expression is an expression that is written as a product of its prime factors.



