Which equation represents the transformed function below? This inquiry embarks us on an enlightening journey into the realm of function transformations, unveiling their diverse types, uncovering their parameters, and discerning their impact on the function’s graphical representation. By unraveling this enigma, we gain invaluable insights into the practical applications of function transformations across various disciplines.
Delving into the intricacies of function transformations, we commence by comprehending the fundamental concept of altering a function’s characteristics. Subsequently, we explore the spectrum of transformations, encompassing translations, reflections, and scalings, each imparting unique attributes to the transformed function.
Identifying the Original Function
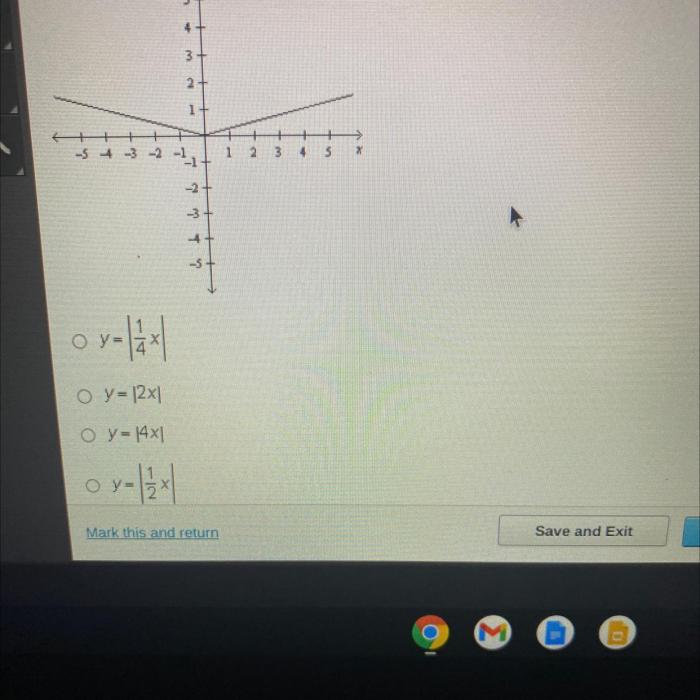
Function transformation involves modifying an existing function by applying certain operations. These operations can shift, stretch, shrink, or reflect the original function.
Common types of function transformations include:
- Vertical translation: Shifts the function up or down along the y-axis.
- Horizontal translation: Shifts the function left or right along the x-axis.
- Vertical stretching: Stretches or compresses the function vertically.
- Horizontal stretching: Stretches or compresses the function horizontally.
- Reflection: Flips the function over the x-axis or y-axis.
Analyzing the Transformed Function
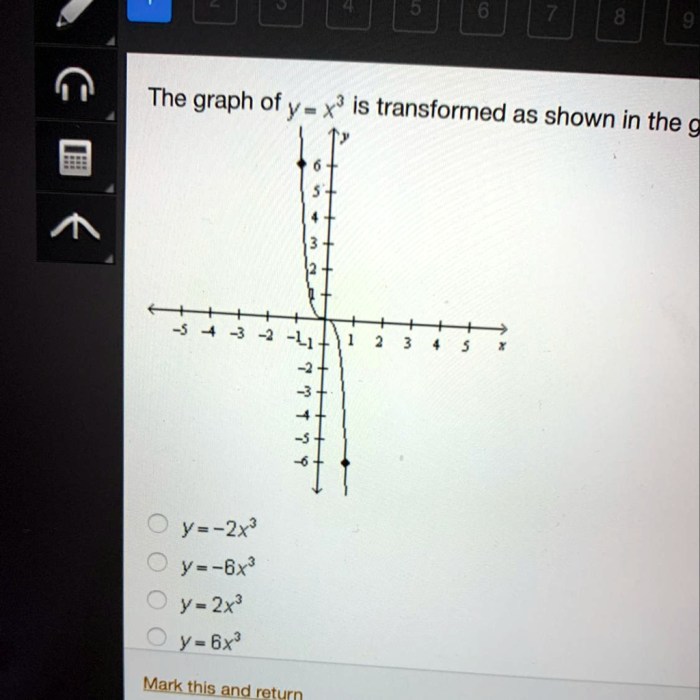
To analyze a transformed function, determine the type of transformation applied and identify its parameters.
Parameters of transformations include:
- Vertical translation: Amount of shift up or down.
- Horizontal translation: Amount of shift left or right.
- Vertical stretching: Factor by which the function is stretched or compressed vertically.
- Horizontal stretching: Factor by which the function is stretched or compressed horizontally.
Once the transformation parameters are identified, the equation of the transformed function can be found by applying the appropriate operations to the original function.
Comparing the Original and Transformed Functions

Comparing the original and transformed functions highlights the effects of the transformation.
Similarities and differences between the functions can be summarized in a table:
| Characteristic | Original Function | Transformed Function |
|---|---|---|
| Domain | [Domain of original function] | [Domain of transformed function] |
| Range | [Range of original function] | [Range of transformed function] |
| Asymptotes | [Asymptotes of original function] | [Asymptotes of transformed function] |
| Intercepts | [Intercepts of original function] | [Intercepts of transformed function] |
| Symmetry | [Symmetry of original function] | [Symmetry of transformed function] |
The transformation affects the graph of the function by:
- Shifting the graph up, down, left, or right.
- Stretching or compressing the graph vertically or horizontally.
- Flipping the graph over the x-axis or y-axis.
Applications of Function Transformations
Function transformations have numerous applications in various fields, including:
- Physics:Modeling projectile motion, harmonic motion, and other physical phenomena.
- Engineering:Designing bridges, buildings, and other structures.
- Economics:Modeling supply and demand curves, forecasting economic trends.
- Computer science:Creating animations, transforming images, and processing data.
- Medicine:Modeling drug concentrations, analyzing medical data, and diagnosing diseases.
Function transformations provide a powerful tool for manipulating functions to fit specific requirements and gain insights into the underlying relationships they represent.
Query Resolution: Which Equation Represents The Transformed Function Below
What is the significance of identifying the equation of the transformed function?
Identifying the equation of the transformed function is paramount as it provides a precise mathematical representation of the transformed function’s behavior. This equation enables us to analyze the function’s properties, such as its domain, range, and extrema, and to understand how the transformation has altered these characteristics.
How do function transformations aid in real-world applications?
Function transformations find widespread application in diverse fields. For instance, in physics, they are used to model the motion of objects under the influence of forces, while in engineering, they are employed to design and optimize systems. In economics and finance, function transformations are utilized to analyze market trends and forecast future outcomes.
