Triangle Congruence Sss Sas Asa Aas Hl Worksheet Answer Key

The Triangle Congruence SSS SAS ASA AAS HL Worksheet Answer Key is an invaluable tool for students and educators alike, providing a comprehensive guide to understanding and applying the fundamental theorems of triangle congruence. This meticulously crafted resource empowers learners to master the intricacies of SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and HL (Hypotenuse-Leg) theorems, equipping them with the knowledge and skills to solve complex geometric problems with confidence.

Within this comprehensive worksheet, students encounter a diverse range of questions designed to test their understanding of each theorem. Clear instructions and illustrative examples guide them through the problem-solving process, fostering a deep comprehension of the underlying concepts. The accompanying answer key serves as an invaluable companion, offering step-by-step solutions to each question, elucidating the reasoning behind each step, and highlighting the crucial concepts involved.

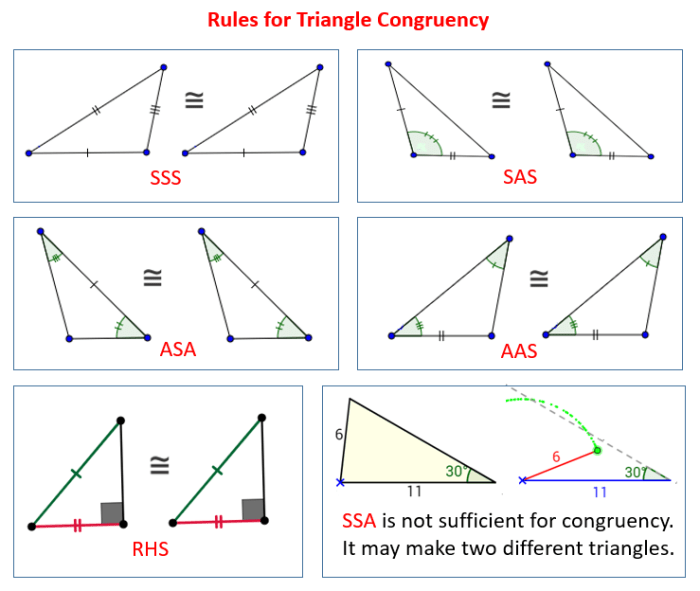
Triangle Congruence Theorems

Triangle congruence theorems establish criteria for determining whether two triangles are congruent, meaning they have the same size and shape.

SSS (Side-Side-Side) Theorem, Triangle congruence sss sas asa aas hl worksheet answer key

If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.

Example: If triangle ABC has sides AB = 5 cm, BC = 7 cm, and AC = 10 cm, and triangle DEF has sides DE = 5 cm, EF = 7 cm, and DF = 10 cm, then triangle ABC is congruent to triangle DEF.

SAS (Side-Angle-Side) Theorem

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.

Example: If triangle ABC has AB = DE, BC = EF, and angle B is congruent to angle E, then triangle ABC is congruent to triangle DEF.

ASA (Angle-Side-Angle) Theorem

If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.

Example: If triangle ABC has angle A congruent to angle D, angle B congruent to angle E, and side AB = DE, then triangle ABC is congruent to triangle DEF.

AAS (Angle-Angle-Side) Theorem

If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.

Limitations:The AAS theorem is only applicable if the non-included side is opposite the congruent angles.

Example: If triangle ABC has angle A congruent to angle D, angle B congruent to angle E, and side AC = DF, then triangle ABC is congruent to triangle DEF.

HL (Hypotenuse-Leg) Theorem

If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent.

Relevance to Right Triangles:The HL theorem is only applicable to right triangles, where the hypotenuse is the longest side.

Example: If triangle ABC is a right triangle with AB (hypotenuse) = DE (hypotenuse) and BC (leg) = EF (leg), then triangle ABC is congruent to triangle DEF.

Triangle Congruence Worksheet

Design:A comprehensive worksheet that covers all triangle congruence theorems.

Content:

Questions testing students’ understanding of each theorem
Clear instructions and examples to guide students

Triangle Congruence Answer Key

Content:

Step-by-step solutions to each question
Explanations of the reasoning behind each solution
Highlighting of important concepts

Interactive Triangle Congruence Tool: Triangle Congruence Sss Sas Asa Aas Hl Worksheet Answer Key

Design:An online tool that allows students to explore triangle congruence theorems.

Features:

Drag-and-drop shapes
Theorem demonstrations
Interactive quizzes
Visually appealing and engaging

Triangle Congruence Applications

Applications:

Architecture: Designing buildings and structures
Engineering: Building bridges and machines
Design: Creating furniture, artwork, and other objects

Benefits:

Solving practical problems
Enhancing problem-solving skills

FAQ Explained

What is the purpose of the Triangle Congruence SSS SAS ASA AAS HL Worksheet Answer Key?

The Triangle Congruence SSS SAS ASA AAS HL Worksheet Answer Key provides a comprehensive guide to understanding and applying the fundamental theorems of triangle congruence, empowering learners to solve complex geometric problems with confidence.

What theorems are covered in the worksheet?

The worksheet covers the SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and HL (Hypotenuse-Leg) theorems.

What is included in the answer key?

The answer key provides step-by-step solutions to each question in the worksheet, elucidating the reasoning behind each step and highlighting the crucial concepts involved.