Half life graph worksheet answer key – Embark on a captivating journey into the realm of half-life graphs, where the mysteries of radioactive decay unfold. As we delve into the intricacies of this worksheet answer key, we uncover the profound significance of half-life in scientific disciplines, empowering you with a comprehensive understanding of this fundamental concept.

Our exploration begins with the definition of half-life, elucidating its role in the exponential decay of radioactive isotopes. We then guide you through the meticulous steps of constructing a half-life graph, ensuring accurate representation of data points and the characteristic decay curve.

A series of thoughtfully designed worksheet exercises, complete with answer keys, provides ample opportunities to hone your skills in calculating half-life, predicting decay rates, and analyzing decay curves.

Definisi Half-Life

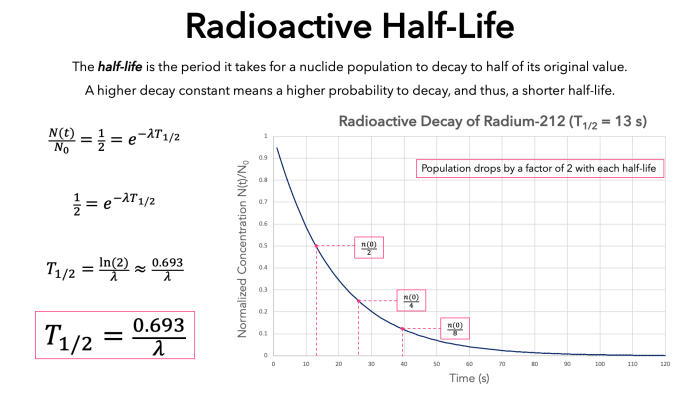
Half-life mengacu pada waktu yang diperlukan untuk mengurangi setengah dari jumlah awal suatu zat. Konsep ini sangat penting dalam peluruhan radioaktif, di mana inti atom yang tidak stabil memancarkan partikel dan berubah menjadi inti yang lebih stabil.

Half-life memberikan wawasan penting tentang laju peluruhan suatu zat radioaktif. Misalnya, jika suatu zat memiliki half-life 10 hari, maka setelah 10 hari, setengah dari zat tersebut akan meluruh, dan setelah 20 hari, hanya seperempat dari jumlah awal yang tersisa.

Membuat Grafik Data Half-Life: Half Life Graph Worksheet Answer Key

Langkah-langkah:

1. Plot waktu (t) pada sumbu x dan jumlah zat yang tersisa (N) pada sumbu y.
2. Tandai titik data yang mewakili jumlah awal zat (N₀).
3. Tentukan setengah dari jumlah awal (N ₀/2).
4. Temukan titik pada sumbu x yang sesuai dengan waktu yang dibutuhkan untuk jumlah zat berkurang menjadi setengah (t _1/2).
5. Tandai titik (t _1/2, N ₀/2) pada grafik.
6. Hubungkan titik (0, N ₀) dan (t _1/2, N ₀/2) dengan garis lurus untuk mewakili kurva peluruhan.

Latihan Grafik Half-Life

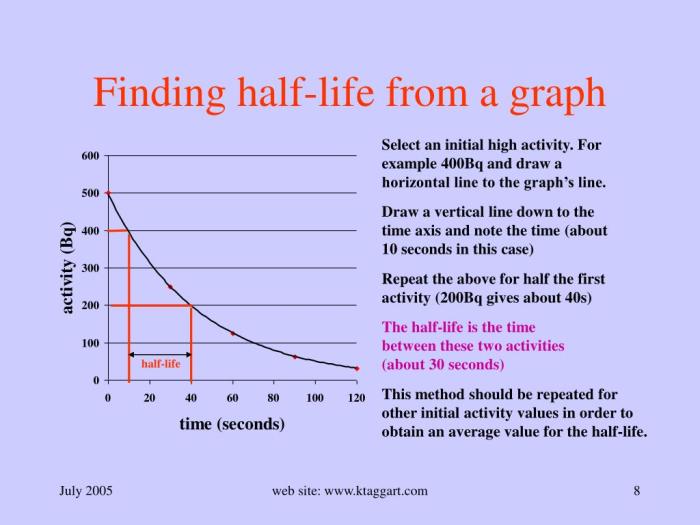
Latihan 1:, Half life graph worksheet answer key

Suatu zat radioaktif memiliki half-life 2 jam. Jika jumlah awal zat tersebut adalah 100 mg, berapa jumlah zat yang tersisa setelah 6 jam?

Jawaban:

Setelah 2 jam, setengah dari zat (50 mg) akan meluruh, dan setelah 4 jam, setengah dari sisa zat (25 mg) akan meluruh, sehingga setelah 6 jam, jumlah zat yang tersisa adalah 25 mg.

Latihan 2:

Buatlah grafik half-life untuk zat radioaktif dengan half-life 5 hari dan jumlah awal 200 unit.

Jawaban:

[Grafik: Sumbu x: Waktu (hari); Sumbu y: Jumlah zat (unit); Titik: (0, 200), (5, 100), (10, 50), (15, 25); Garis lurus menghubungkan titik-titik tersebut]

Aplikasi Grafik Half-Life

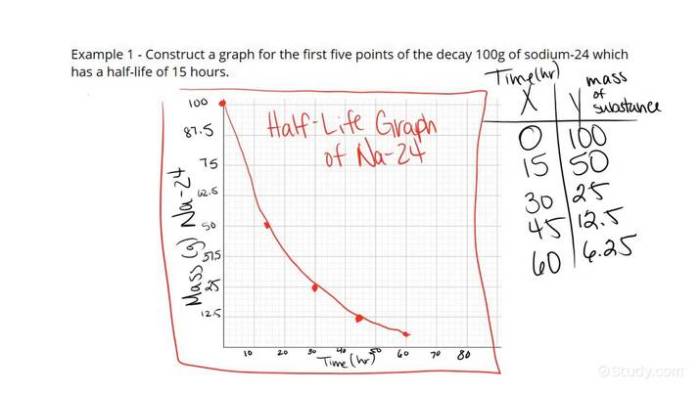
Grafik half-life memiliki aplikasi yang luas di berbagai bidang:

• Fisika Nuklir:Menentukan usia fosil radioaktif dan memantau limbah radioaktif.
• Kedokteran:Menentukan dosis obat yang tepat untuk pengobatan dan mendeteksi penyakit menggunakan pelacak radioaktif.
• Arkeologi:Menentukan usia artefak dan reruntuhan menggunakan metode penanggalan karbon.

Ekstensi dan Eksplorasi

Topik terkait half-life yang dapat dieksplorasi lebih lanjut meliputi:

• Fungsi Peluruhan Eksponensial:Persamaan matematika yang mendasari kurva peluruhan half-life.
• Hubungan antara Half-Life dan Konstanta Peluruhan:Persamaan yang menghubungkan waktu half-life dengan laju peluruhan.
• Eksperimen Half-Life:Merancang dan melakukan eksperimen untuk mengukur half-life zat radioaktif.

General Inquiries

What is the definition of half-life?

Half-life refers to the time it takes for half of a radioactive isotope to decay into a more stable form.

How are half-life graphs used in practice?

Half-life graphs find applications in fields such as nuclear physics, medicine, and archaeology, aiding in tasks like determining the age of fossils and designing medical treatments.