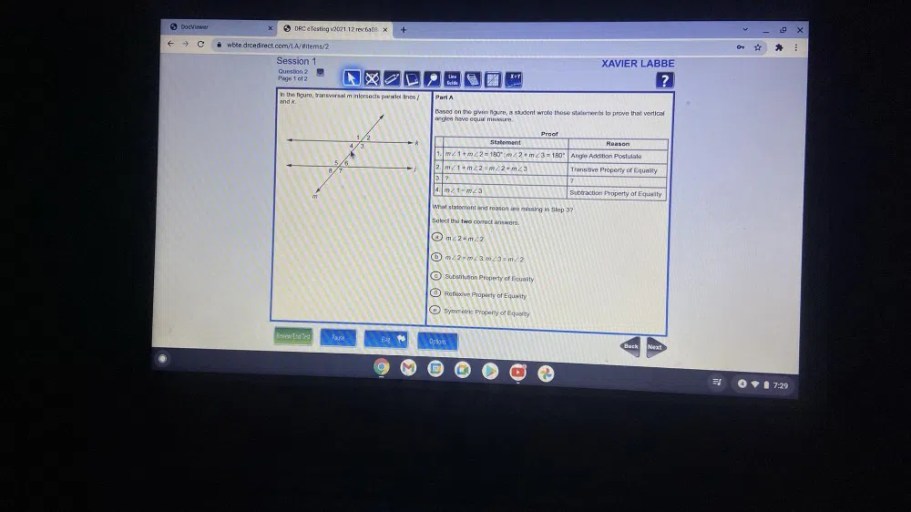
Select the postulate of equality or inequality that is illustrated. – Introducing the fundamental principles of mathematics, we delve into the postulates of equality and inequality, exploring their significance and applications. These postulates serve as the cornerstone of mathematical reasoning, enabling us to establish relationships between numbers and expressions.
The postulate of equality asserts that if two expressions are equal to a third expression, then they are equal to each other. This principle forms the basis for algebraic manipulations and equations. On the other hand, the postulate of inequality states that if one expression is greater than a second expression, and the second expression is greater than a third expression, then the first expression is greater than the third expression.
This postulate underpins the ordering of numbers and the comparison of expressions.
Postulate of Equality
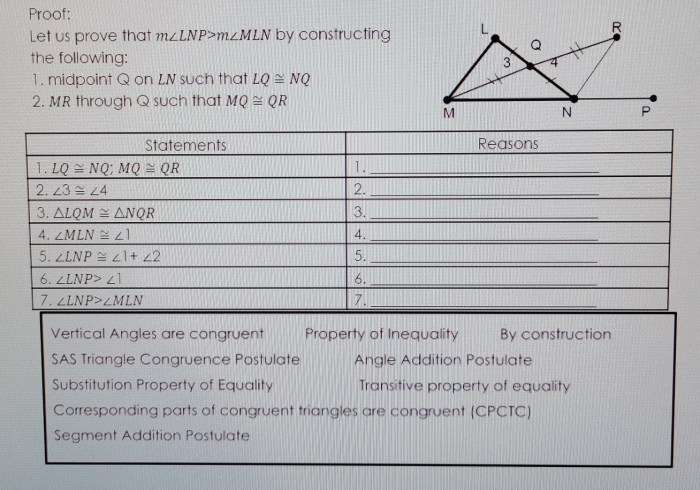
The postulate of equality states that if two mathematical expressions are equal to a third expression, then they are equal to each other. This postulate is essential for solving equations and inequalities, as it allows us to replace one expression with another without changing the value of the equation or inequality.
Examples of the Postulate of Equality
- If a = b and b = c, then a = c.
- If x + 5 = 10, then x = 10 – 5 = 5.
- If 2y – 3 = 7, then 2y = 7 + 3 = 10, so y = 10 / 2 = 5.
Importance of the Postulate of Equality, Select the postulate of equality or inequality that is illustrated.
The postulate of equality is one of the most fundamental postulates in mathematics. It allows us to solve equations and inequalities, which are essential for solving a wide variety of mathematical problems. Without the postulate of equality, it would be impossible to do many of the basic operations of mathematics.
Postulate of Inequality
The postulate of inequality states that if two mathematical expressions are not equal to each other, then one expression must be greater than the other. This postulate is essential for comparing numbers and expressions, as it allows us to determine which expression is larger or smaller.
Examples of the Postulate of Inequality
- If a > b, then b< a.
- If x + 5 > 10, then x > 10 – 5 = 5.
- If 2y – 3< 7, then 2y < 7 + 3 = 10, so y < 10 / 2 = 5.
Importance of the Postulate of Inequality
The postulate of inequality is another fundamental postulate in mathematics. It allows us to compare numbers and expressions, which is essential for solving a wide variety of mathematical problems. Without the postulate of inequality, it would be impossible to do many of the basic operations of mathematics.
Comparison of the Postulates

The postulate of equality and the postulate of inequality are two of the most fundamental postulates in mathematics. They are both essential for solving equations and inequalities, and they both play an important role in a wide variety of mathematical problems.
Similarities
- Both postulates are based on the concept of equality.
- Both postulates are essential for solving equations and inequalities.
- Both postulates are used in a wide variety of mathematical problems.
Differences
- The postulate of equality states that if two expressions are equal to a third expression, then they are equal to each other. The postulate of inequality states that if two expressions are not equal to each other, then one expression must be greater than the other.
- The postulate of equality is used to solve equations. The postulate of inequality is used to solve inequalities.
How the Two Postulates Are Used Together
The postulate of equality and the postulate of inequality are often used together to solve mathematical problems. For example, we can use the postulate of equality to solve the equation x + 5 = 10. We can then use the postulate of inequality to determine whether x is greater than or less than 5.
Applications of the Postulates

The postulate of equality and the postulate of inequality are used in a wide variety of applications. For example, they are used in:
- Algebra
- Geometry
- Calculus
- Statistics
The postulate of equality is used to solve equations, which are used in a wide variety of applications. For example, equations are used to solve problems in physics, engineering, and economics. The postulate of inequality is used to compare numbers and expressions, which is essential for solving a wide variety of mathematical problems.
For example, inequalities are used to solve problems in optimization, finance, and computer science.
Questions and Answers: Select The Postulate Of Equality Or Inequality That Is Illustrated.
What is the difference between the postulate of equality and the postulate of inequality?
The postulate of equality states that if two expressions are equal to a third expression, then they are equal to each other. The postulate of inequality states that if one expression is greater than a second expression, and the second expression is greater than a third expression, then the first expression is greater than the third expression.
How are the postulates of equality and inequality used in real-world applications?
The postulates of equality and inequality are used in a wide range of real-world applications, including science, engineering, and finance. For example, in physics, the postulate of equality is used to derive equations that describe the motion of objects. In engineering, the postulate of inequality is used to design structures that can withstand certain loads.
